SMS:TUFLOW Inlet Database
TUFLOW supports several types of inlets that connect 1D pipe network domains to 2D overland domains. These include circular, rectangular, and weir. TUFLOW now also supports the ability to define depth vs flow curves to allow for more flexibility. The user defined inlet information is stored in an inlet database.
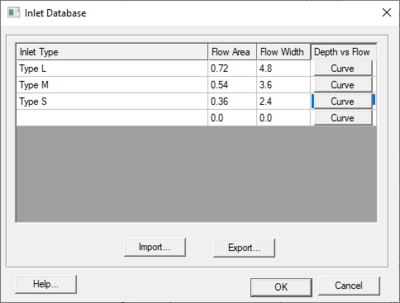
The inlet database stores information about the user defined inlet types. This information includes the flow area, width, and the depth vs flow curve. The flow area is used to compute the velocities in the inlet channel and the width is used to determine how many 2D cells to connect the inlet to. For more information about how TUFLOW uses the inlet database, see the TUFLOW documentation.
To define the Inlet Database
- Create a 1D Network coverage and an arc.
- Double-click on the end node of an arc (which is where inlets are defined)
- Change the inlet type to "Inlet — From Database"
- Click on the button labeled Inlet Database...
- In the Inlet Database dialog that comes up, define the type (name), flow area, flow width, and curve for each of the inlets to be defined.
To use an inlet from an Inlet Database
- Create a 1D Network coverage and an arc.
- Double-click on the end node of an arc (which is where inlets are defined)
- Change the inlet type to "Inlet – From Database"
- Select the inlet type by name in the combo-box labeled Inlet Database Name.
Importing/Exporting the Inlet Database
From the Inlet Database dialog, it is possible to export or import the database in to the format used by TUFLOW (two or more csv files). This format is very easy to create or use for graphs using a spreadsheet program. For more information on this format, see the TUFLOW documentation.
Related Topics
| [hide] SMS – Surface-water Modeling System | ||
|---|---|---|
| Modules: | 1D Grid • Cartesian Grid • Curvilinear Grid • GIS • Map • Mesh • Particle • Quadtree • Raster • Scatter • UGrid |  |
| General Models: | 3D Structure • FVCOM • Generic • PTM | |
| Coastal Models: | ADCIRC • BOUSS-2D • CGWAVE • CMS-Flow • CMS-Wave • GenCade • STWAVE • WAM | |
| Riverine/Estuarine Models: | AdH • HEC-RAS • HYDRO AS-2D • RMA2 • RMA4 • SRH-2D • TUFLOW • TUFLOW FV | |
| Aquaveo • SMS Tutorials • SMS Workflows | ||