GMS:Strike Dip Markov Chain
| T-PROGS | |
|---|---|
| Links | |
| T-PROGS | |
| Strike Dip Markov Chain | |
| Vertical Markov Chain | |
| TSIM | |
Once the vertical Markov chains have been defined, the Strike (X) Markov Chains dialog become available. This dialog has the same general setup as the Vertical Markov Chain dialog.
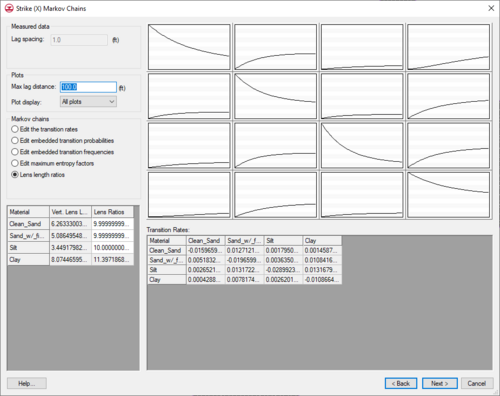
Strike (X) Markov Chains
There are three minor differences between this dialog and the vertical dialog. The first difference is in the Markov Chains section. The option, Lens width ratios, replaces the Fit curves to a discrete lag option. The Fit curves to a discrete lag option is not applicable because horizontal measured transition probability curves do not exist due to lack of data in the horizontal direction. The Lens width ratios option is the default option and should be used in most cases. This option allows applying the transition data entered in the vertical direction to the horizontal direction. The proportion data are directly inherited from the vertical data.
The second change is in the spreadsheet section. Rather than entering the mean lengths, enter a ratio corresponding to the ratio of the lens length in the x direction to the lens length in the z direction. For example, if the lens length for material A is 5 feet in the z direction and 10.0 is entered for the ratio, then the lens length in the x direction would be 50 feet. The Lens Width Ratios option is particularly useful because the only required input is lens length ratios for the non-background materials. The remaining data are all inherited from the vertical data. The third change is in the plot section. Due to the lack of measured data in the horizontal direction, each plot contains only one curve: the Markov chain curve.
Vertical→Lateral Data Conversion
Typical site stratigraphic data is conducive to developing vertical spatial variability. However, rarely is the quantity of data adequate to develop an accurate model in the lateral directions. The combination of Walther’s Law and the transition probability approach allows for a logical method of developing lateral spatial variability from vertical spatial variability. Walther’s Law states that vertical successions of deposited facies represent the lateral succession of environments of deposition. Therefore, a logical method of generating a 3-D model of spatial variability would be first to develop a 1-D Markov chain in the vertical direction based on site data, assuming there is such data. Second, using Walther’s Law and geologic knowledge, one can develop lateral, strike and dip, Markov chains of spatial variability. However, one issue that arises when applying vertical transition trends to lateral directions is how to cope with asymmetric vertical trends like fining upwards. For example, if in the vertical direction, sand tends to deposit on gravel as would be typical in a fluvial deposition, there will be a transition rate associated with the transition of "sand→gravel" and "gravel→sand". The transition of "gravel→sand" will be greater than "sand→gravel" because of the fining upward trend. However, in the lateral direction, which of these transition rates should be applied? Although the trend of sand next to gravel remains in the lateral direction, the transition rates of "sand→gravel" and "gravel→sand" should be equivalent or symmetric as defined by:
The strategy for averaging the vertical transition rates to come up with the lateral rates is given in the three steps below.
- Compute the lower-half rate (R-ls) that will satisfy symmetry with the upper-half rate (R-u) for the vertical data using the symmetry relation.
- Set the lower-half rate for the lateral direction (R'-l) equal to (R-l + R-ls)/2
- Compute the upper-half rate for the lateral direction (R'-u) that will satisfy symmetry with the new lower-half rate (R'-l) using the symmetry relation.
In addition to the averaging technique applied to the off-diagonal terms of the lateral transition rates, an adjustment was made to the diagonal terms of the rate matrix. It will be remembered that the diagonal terms correlate to the average mean lengths by
Generally, in depositional patterns, lateral mean lengths are larger than their counterparts. Therefore, the lateral mean lengths generally need to be increased by a prescribed factor F. This factor F is equal to the ratio of the lateral mean lengths/vertical mean lengths. If the mean length for category K increases by a factor F, the corresponding transition rate will decrease by that same factor F. And the row sum for category K must therefore decrease by the factor F.
Dip (Y) Markov Chains
The Dip (Y) Markov Chain dialog has an identical appearance and functionality as the Strike (X) Markov Chains dialog.
| [hide]GMS – Groundwater Modeling System | ||
|---|---|---|
| Modules: | 2D Grid • 2D Mesh • 2D Scatter Point • 3D Grid • 3D Mesh • 3D Scatter Point • Boreholes • GIS • Map • Solid • TINs • UGrids | |
| Models: | FEFLOW • FEMWATER • HydroGeoSphere • MODAEM • MODFLOW • MODPATH • mod-PATH3DU • MT3DMS • MT3D-USGS • PEST • PHT3D • RT3D • SEAM3D • SEAWAT • SEEP2D • T-PROGS • ZONEBUDGET | |
| Aquaveo | ||