GMS:Strike Dip Markov Chain: Difference between revisions
From XMS Wiki
Jump to navigationJump to search
No edit summary Tag: Manual revert |
|||
| (22 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
{{T-PROGS Links}} | {{T-PROGS Links}} | ||
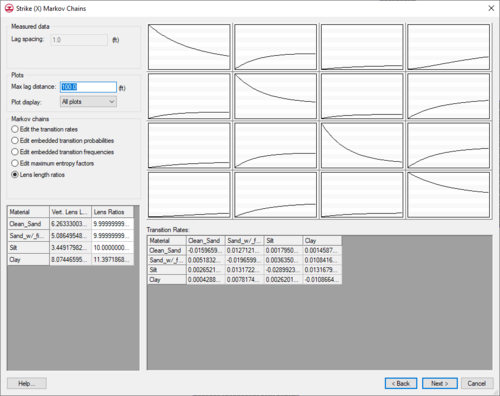
Once the vertical Markov chains have been defined, | Once the vertical Markov chains have been defined, the ''Strike (X) Markov Chains'' dialog become available. This dialog has the same general setup as the [[GMS:Vertical Markov Chain|''Vertical Markov Chain'']] dialog. | ||
==Strike (X) Markov Chains== | ==Strike (X) Markov Chains== | ||
[[Image: | [[Image:Markov chains x.png|thumb|500px|''Strike/Dip Markov chain dialog''.]] | ||
There are three minor differences between this dialog and the vertical dialog. The first difference is in the [[GMS:Vertical Markov Chain|Markov Chains section]]. The option, Lens width ratios, replaces the Fit curves to a discrete lag option. The Fit curves to a discrete lag option is not applicable because horizontal measured transition probability curves do not exist due to lack of data in the horizontal direction. The Lens width ratios option is the default option and should be used in most cases. This option allows | There are three minor differences between this dialog and the vertical dialog. The first difference is in the [[GMS:Vertical Markov Chain|''Markov Chains'' section]]. The option, ''Lens width ratios'', replaces the ''Fit curves to a discrete lag'' option. The ''Fit curves to a discrete lag'' option is not applicable because horizontal measured transition probability curves do not exist due to lack of data in the horizontal direction. The ''Lens width ratios'' option is the default option and should be used in most cases. This option allows applying the transition data entered in the vertical direction to the horizontal direction. The proportion data are directly inherited from the vertical data. | ||
The second change is in the [[GMS:Vertical Markov Chain| | The second change is in the [[GMS:Vertical Markov Chain|spreadsheet section]]. Rather than entering the mean lengths, enter a ratio corresponding to the ratio of the lens length in the x direction to the lens length in the z direction. For example, if the lens length for material A is 5 feet in the z direction and 10.0 is entered for the ratio, then the lens length in the x direction would be 50 feet. The ''Lens Width Ratios'' option is particularly useful because the only required input is lens length ratios for the non-background materials. The remaining data are all inherited from the vertical data. The third change is in the [[GMS:Vertical Markov Chain|plot section]]. Due to the lack of measured data in the horizontal direction, each plot contains only one curve: the Markov chain curve. | ||
===Vertical→Lateral Data Conversion=== | ===Vertical→Lateral Data Conversion=== | ||
Typical site stratigraphic data is conducive to developing vertical spatial variability. However, rarely is the quantity of data adequate to develop an accurate model in the lateral directions. The combination of Walther’s Law and the transition probability approach allows for a logical method of developing lateral spatial variability from vertical spatial variability. Walther’s Law states that vertical successions of deposited facies represent the lateral succession of environments of deposition. Therefore, a logical method of generating a 3-D model of spatial variability would be first to develop a 1-D Markov chain in the [[GMS:Vertical Markov Chain|vertical direction]] based on site data, assuming there is such data. Second, using Walther’s Law and geologic knowledge, one can develop lateral, strike and dip, Markov chains of spatial variability. However, one issue that arises when applying vertical transition trends to lateral directions is how to cope with asymmetric vertical trends like fining upwards. For example, if in the vertical direction, sand tends to deposit on gravel as would be typical in a fluvial deposition, there will be a transition rate associated with the transition of "sand→gravel" and "gravel→sand". The transition of "gravel→sand" will be greater than "sand→gravel" because of the fining upward trend. However, in the lateral direction, which of these transition rates should be applied? Although the trend of sand next to gravel remains in the lateral direction, the transition rates of "sand→gravel" and "gravel→sand" should be equivalent or symmetric as defined by | Typical site stratigraphic data is conducive to developing vertical spatial variability. However, rarely is the quantity of data adequate to develop an accurate model in the lateral directions. The combination of Walther’s Law and the transition probability approach allows for a logical method of developing lateral spatial variability from vertical spatial variability. Walther’s Law states that vertical successions of deposited facies represent the lateral succession of environments of deposition. Therefore, a logical method of generating a 3-D model of spatial variability would be first to develop a 1-D Markov chain in the [[GMS:Vertical Markov Chain|vertical direction]] based on site data, assuming there is such data. Second, using Walther’s Law and geologic knowledge, one can develop lateral, strike and dip, Markov chains of spatial variability. However, one issue that arises when applying vertical transition trends to lateral directions is how to cope with asymmetric vertical trends like fining upwards. For example, if in the vertical direction, sand tends to deposit on gravel as would be typical in a fluvial deposition, there will be a transition rate associated with the transition of "sand→gravel" and "gravel→sand". The transition of "gravel→sand" will be greater than "sand→gravel" because of the fining upward trend. However, in the lateral direction, which of these transition rates should be applied? Although the trend of sand next to gravel remains in the lateral direction, the transition rates of "sand→gravel" and "gravel→sand" should be equivalent or symmetric as defined by: | ||
<!--[[Image:t-progs_eq4.png]] | <!--[[Image:t-progs_eq4.png]] | ||
<math>r_{jk}=\frac{p_k}{p_j}r_{kj}</math>--> | <math>r_{jk}=\frac{p_k}{p_j}r_{kj}</math>--> | ||
[[Image:strikedipchain1.jpg]] | :[[Image:strikedipchain1.jpg]] | ||
The strategy for averaging the vertical transition rates to come up with the lateral rates is given in the three steps below. | The strategy for averaging the vertical transition rates to come up with the lateral rates is given in the three steps below. | ||
| Line 27: | Line 28: | ||
<!--[[Image:t-progs_eq3.png]] | <!--[[Image:t-progs_eq3.png]] | ||
<math>\bar{L}_{j,\phi}=\frac{-1}{r_{jj,\phi}}</math>--> | <math>\bar{L}_{j,\phi}=\frac{-1}{r_{jj,\phi}}</math>--> | ||
[[Image:verticalchain3.jpg]] | :[[Image:verticalchain3.jpg]] | ||
Generally, in depositional patterns, lateral mean lengths are larger than their counterparts. Therefore, the lateral mean lengths generally need to be increased by a factor F | Generally, in depositional patterns, lateral mean lengths are larger than their counterparts. Therefore, the lateral mean lengths generally need to be increased by a prescribed factor F. This factor F is equal to the ratio of the lateral mean lengths/vertical mean lengths. If the mean length for category K increases by a factor F, the corresponding transition rate will decrease by that same factor F. And the row sum for category K must therefore decrease by the factor F. | ||
==Dip (Y) Markov Chains== | ==Dip (Y) Markov Chains== | ||
The | The ''Dip (Y) Markov Chain'' dialog has an identical appearance and functionality as the ''Strike (X) Markov Chains'' dialog. | ||
{{Navbox GMS}} | {{Navbox GMS}} | ||
[[Category:T-PROGS]] | [[Category:T-PROGS]] | ||
[[Category:T-PROGS Dialogs]] | |||
[[Category:Equations|Strike]] | |||