GMS:RT3D Reaction Packages
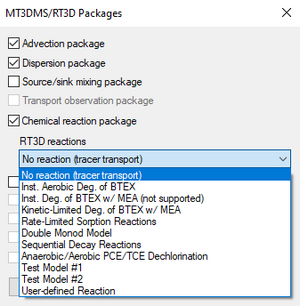
When using RT3D, GMS provides a number of reaction packages. Reaction packages are selected in the MT3DMS/Packages dialog. If one of these reactions is selected, the names of the species and the names of the reaction parameters are automatically determined by GMS.
- "No reaction (tracer transport)"
- "Inst. Aerobic Deg. of BTEX" – Instantaneous aerobic degradation of hydrocarbons. Creates two species: BTEX and Oxygen.
- "Inst. Deg. of BTEX w/MEA (not supported)"
- "Kinetic-Limited Deg. of BTEX w/MEA" – Creates species: BTEX, Oxygen, Nitrate, Iron(Fe2+), Sulfate, and Methane.
- "Rate-Limited Sorption Reactions" – Creates two species: Aqueous conc and Solid conc. See below.
- "Double Monod Model" – See below.
- "Sequential Decay Reactions" – See below.
- "Anaerobic/Aerobic PCE/TCE Dechlorination" – Creates two species: Electron Acceptor and Soil-phase bacteria.
- Test Model #1
- Test Model #2
- "User-defined Reaction" – Allows using a reaction defined by the user. See below.
Inst. Aerobic Deg. of BTEX
The reaction model used here simulates the instantaneous degradation of fuel hydrocarbons under aerobic conditions based on the following reaction (benzene basis):
Therefore, the mass ratio of benzene to oxygen, F, is 3.08 (i.e., 3.08g of oxygen to 1g of benzene). The instantaneous removal of either contaminant (H) or oxygen (O) is dictated by the following algorithm, where t refers to a particular time step:
- and , when
- and , when
Given this algorithm, either hydrocarbon or oxygen concentration in a given grid cell will be reduced to zero at each time step, depending on which component is stoichiometrically limiting in the prior time step.
Kinetic-Limited Deg. of BTEX w/MEA
The reaction that will be simulated is biodegradation of BTEX compounds via different aerobic/anaerobic pathways using multiple electron acceptors. Five different processes considered in this model are Aerobic Respiration (AR), Denitrification (DN), Iron (III) Reduction (IR), Sulfate Reduction (SR), and Methanogenesis (MG). All of these biochemical reactions are assumed to occur in the aqueous phase, mediated by the existing subsurface microbes, and are expected to happen in the following sequence:
The following reaction kinetic framework is used to model the degradation rate of hydrocarbon via different electron acceptor pathways:
- where
- rHC,O2 is the rate at which hydrocarbon is destroyed by utilizing oxygen,
- rHC,NO3 is the rate at which hydrocarbon is destroyed by utilizing Nitrate,
- rHC,Fe2+ is the rate at which hydrocarbon is destroyed by producing Fe2+ (or utilizing Fe3+),
- rHC,SO4 is the rate at which hydrocarbon is destroyed by utilizing sulfate,
- rHC,CH4 is the rate at which hydrocarbon is destroyed by producing methane,
- [O2] is the oxygen concentration [ML-3],
- kO2 is the first-order rate constant [T-1],
- KO2 is the Monod half saturation constant [ML-3] (by setting all the half-saturation constants to a small value, zero-order dependency can be simulated with respect to the electron donor and hence a first-order degradation model with respect to hydrocarbon; the default values simulate this option), and
- Ki,o2 is the oxygen inhibition constant [ML-3] (by setting all inhibition constants to a small value, reactions can be forced to occur in a sequential fashion; the default values simulate this process). Similar nomenclature is used to identify other Monod constants and inhibition coefficients.
Since the concentrations of Fe3+ and CO2 are not readily measurable under normal field conditions, these terms were replaced with the “assimilative capacity” for iron reduction and methanogenesis, defined as the following:
- where [Fe2+max] and [CH4,max] are the maximum possible aquifer levels of these species that represent the aquifer’s maximum capacity for iron reduction and methanogenesis. Note: the concentration of CO2 used here is the CO2 evolved while the hydrocarbon is destroyed via methanogenesis, which may be thought of as the “Methanogenic Capacity” (MC) of the aquifer. Using these relations, iron (III) reduction and methanogenesis processes may be related back to measurable Fe2+ and CH4 concentration levels.
The total rate of hydrocarbon destruction, via all the above described processes, is the sum of each of the individual rates and is given as the following:
Rates of electron acceptor utilization are given as the corresponding rate of hydrocarbon destruction multiplied by the appropriate yield coefficient (Y):
The yield values (the mass ratio of electron acceptors removed or metabolic byproducts produced to total BTEX degraded) are as follows: Y02/HC = 3.14, YNO3/HC = 4.9, YFe2+/HC = 21.8, YSO4/HC = 4.7, and YCH4/HC = 0.78. Typical values of all inhibition coefficients, except for KiFe3+, should be in the range of 1.0 to 0.01 mg/L. KiFe3+ should always be set around 40% to 80% of the max Fe2+ value. Monod half-saturation constants should be in the range of 1.0 to 0.1 mg/L.
As pointed out in Lu et al. [1], it is important to note that this model is based on several assumptions. The model should be used with caution only at sites where these assumptions are valid.
In summary, the key assumptions used in the model are: (1) the fuel chemical species benzene, toluene, ethylbenzene, and xylene are assumed to degrade at similar rates and, hence, are combined and modeled as a single electron donor species BTEX; (2) production of Fe2+ and methane are restricted at a node to a “maximum-observed level”; however, the model assumes that an infinite supply of electron acceptors will be available for iron-reduction and methanogenic reactions; (3) more complex processes are not considered; these include processes such as the rate-limited interaction of bioavailable, solid-phase Fe3+ and aqueous-phase Fe2+, interaction of oxygen and Fe2+, and/or variations in the spatial pattern of methanogenic activity and CO2 availability; (4) growth and decay of various microbial populations and their interactions with contaminants and aquifer solids are assumed to be negligible; and (5) all BTEX decay reactions are approximated as first-order reactions, and, hence, the model ignores the Monod limitation due to the electron donor (BTEX) availability. Fortunately, these assumptions are expected to be reasonable approximations for most field sites. However, there will always be some exceptions.
Rate-Limited Sorption Reactions
The fate and transport of an organic pollutant in subsurface environments is often highly dependent on its sorption characteristics. Under most natural groundwater flow conditions, the partitioning of contaminants between the solid and aqueous phases can be assumed to be at a local equilibrium. Thus, the more widely used retardation approach for modeling sorption may provide an adequate description for the overall transport. However, the equilibrium assumption may fail when external pumping and injection stresses are imposed on an aquifer (e.g. using a pump-treat system). This would lead to some well-known conditions such as the plume tailing effect (i.e., low contaminant levels always observed at the extraction well) and/or the rebounding effect (i.e., the aquifer seems to be clean but the aqueous concentrations start to increase immediately after stopping the treatment system). These conditions cannot be simulated using the standard linear retardation approach since they require a mass-transfer description for the sorption reactions.
In the mass-transfer limited sorption model, the exchange of contaminants between the soil and groundwater is assumed to be rate limited. The rate of exchange is dictated by the value of the mass-transfer coefficient. When the mass-transfer rate is high (relative to the overall transport), the rate-limited model relaxes to the retardation model. On the other end of the spectrum, a very low mass-transfer coefficient would mimic fully sequestered conditions where the contaminants in the soil phase are assumed to be irreversibly adsorbed and trapped into the soil pores. Under this extreme condition, it might be possible to simply clean the groundwater plume and leave the sequestered soil contaminant in the aquifer because the sorbed contaminants may not pose any potential risk to the environment. In either of the extreme conditions, pump-and-treat is the best option to remediate the groundwater plume. Unfortunately, in most instances, the mass-transfer coefficient is expected to lie in an intermediate range, causing the well-known limitations to the pump-and-treat system.
When sorption is assumed to be rate limited, it is necessary to track contaminant concentrations in both mobile (groundwater) and immobile (soil) phases. Following Haggerty and Gorelick’s (1994) approach [2], the fate and transport of a sorbing solute at aqueous and soil phases can be predicted using the following transport equations:
- where
- C is the concentration of the contaminant in the mobile-phase [ML-3],
- is the concentration of the contaminant in the immobile phase (mass of the contaminants per unit mass of porous media, [MM-1]),
- r is the bulk density of the soil matrix,
- Φ is the soil porosity,
- ξ is the first-order, mass-transfer rate parameter [T-1], and
- λ is the linear partitioning coefficient (which is equal to the linear, first-order sorption constant Kd) [L3M-1].
It can be mathematically shown that the above model formulation relaxes to the retardation model when the value of x becomes high.[3]
The mass-transfer model discussed above has been implemented as an RT3D reaction package (one mobile species and one immobile species). After employing reaction-operator splitting, the reaction package for the problem reduces to the following:
These two differential equations are coded into the model #4 designated as the rate-limited sorption reaction module.
Double Monod Model
Methods for enhancing in situ bioremediation of subsurface soil and groundwater involve injection or infiltration of a carbon source (or electron donor), nutrients, and other electron acceptors to stimulate the growth of native microbes. In addition, bioengineered suspension cultures of contaminant degrading organisms may be also added to increase the amount of attached and suspended biomass in the subsurface. These two types of active remediation techniques can be used to bioremediate contaminated source zones or to establish a biobarrier to prevent plume migration and/or to enhance plume attenuation. The successful use of subsurface microbes for bioremediation requires an understanding of coupled flow, transport, and reaction processes that control bacterial growth and migration patterns. The Dual-Monod model, available in the RT3D code, can be used to develop such understanding by simulating the coupled reactive transport and microbial growth. The model is developed in a general format; therefore, the interaction between any electron donor and acceptor mediated by any type of microbial population can be simulated by varying appropriate kinetic constants. Advanced users can modify this basic formulation and couple it with other packages, such as the sorption package, to simulate more realistic bioremediation scenarios (any such modified reaction models can be easily implemented via the user-defined reaction option).
Assuming the linear-equilibrium model for modeling sorption, and the Dual-Monod model for modeling bacterial growth, the fate and transport equation for an electron donor (hydrocarbon, for example) in a multi-dimensional saturated porous media can be written as follows:
- where
- [D] is the electron donor concentration in the aqueous phase [ML-3]
- [Ds] is the donor concentration in the sources/sinks [ML-3],
- Dij is the dispersion coefficient;
- [X] is the aqueous phase bacterial cell concentration [ML-3],
- X̃ is the solid-phase cell concentration (mass of bacterial cells per unit mass of porous media [MM-1]),
- [A] is the electron acceptor concentration in the aqueous phase [ML-3],
- RH is the retardation coefficient of the hydrocarbon,
- KD is the half-saturation coefficient for the electron donor [ML-3],
- KA is the half-saturation coefficient for the electron acceptor [ML-3], and
- μm is the contaminant utilization rate [T-1].
The model assumes that the degradation reactions occur only in the aqueous phase, which is usually a conservative assumption.
The fate and transport of the electron donor (oxygen, for example) can be modeled using this equation:
- where
- YA/D is the stoichiometric yield coefficient, and RA is the retardation coefficient of the electron acceptor.:
The fate and transport of bacteria in the aqueous phase can be described using this equation:
- where
- Katt is the bacterial attachment coefficient [T-1],
- Kdet is the bacterial detachment coefficient [T-1], and
- Ke is the endogenous cell death or decay coefficient [T-1].
The growth of attached-phase bacteria can be described using an ordinary differential equation of the form:
The conceptual model used here for representing attached bacteria cells is similar to the macroscopic model described by Baveye and Valocchi (1989). [4] The model also assumes first-order kinetic expressions for representing bacterial attachment and detachment processes (Taylor and Jaffé, 1990; and Hornberger et al., 1992).[5] [6] Permeability and porosity changes caused by bacterial growth are ignored in this formulation. However, if required, macroscopic models for biomass-affected porous-media properties described by Clement et al. (1996) may be integrated within this modeling approach.[7] It should be noted that a lot of active research is currently underway to gain an increased understanding of bacteria transport in porous media because currently available bacterial transport models (including the model used here) are arguably approximate. Therefore, application of this model to real situations should be always supported by field- or laboratory-scale data.
The reactive-transport model discussed above was set up as a RT3D reaction package with three mobile species (to represent electron donor, electron acceptor, and aqueous bacteria) and one immobile species (to represent attached soil bacteria). After employing the reaction-operator splitting strategy, the reaction package for the problem reduces to the following:
These four equations are coded into the double-monod reaction module.
Sequential Decay Reactions
The reaction being simulated is anaerobic PCE dechlorination with sequential, first-order, degradation kinetics. Degradation of PCE all the way to VC is assumed to be anaerobically favorable and the degradation kinetics are assumed to be first order in nature.
The following set of equations describes the reaction kinetics framework:
Kinetic Constants (to be manually entered):
| Constant | Value | Designation |
|---|---|---|
| k1 | 0.005 day-1 | PCE anaerobic constant |
| k2 | 0.003 day-1 | TCE anaerobic constant |
| k3 | 0.002 day-1 | DCE anaerobic constant |
| k4 | 0.001 day-1 | VC anaerobic constant |
The following constants (yields in mg/mg basis) are fixed internally:
| Constant | Value | Designation |
|---|---|---|
| YTCE/PCE | 0.7920 | TCE:PCE stoichiometric yield |
| YDCE/TCE | 0.7377 | DCE:TCE stoichiometric yield |
| YVC/DCE | 0.6445 | VC:DCE stoichiometric yield |
User-Defined Reactions
| This contains information for a feature that is not currently supported. Technical support is not available for projects using this feature. |
User-defined reaction packages can be created using one of two approaches: the dynamically linked library (DLL) option or the linked subroutine option. With the DLL option, the subroutine for the reaction package is compiled as a stand-alone DLL. The DLL is then copied to the same directory as the RT3D executable, and the DLL is automatically launched by RT3D when RT3D is executed. The DLL can be recompiled, or a new DLL can be used simply by copying the new DLL to the same directory as the RT3D executable and naming it appropriately. The RT3D executable does not need to be recompiled.
With the linked subroutine option, the code for the new reaction subroutine is compiled and linked with the rest of the RT3D source code (or the RT3D library made for a specific computer platform). In other words, the RT3D executable must be recompiled each time the reaction package is modified.
Because of the portability of the developed reaction package, the DLL option is the more convenient of the two options. However, the DLL option is only available on the Windows platform. It is not available on Unix.
Reaction module developers are considered advanced users of the RT3D code. The required background is as follows:
- Should have a basic understanding of the functionality of RT3D code and understand how different types of components (mobile and immobile) are mathematically described within RT3D modeling framework.
- Should be familiar with GMS and be able to create MODFLOW and RT3D input files with little effort.
- Should be familiar with the data structure of RT3D input files such as BTN, SSM, and RCT files.
- Should have a basic understanding of the FORTRAN language and have access to A Digital FORTRAN compiler (or a UNIX-system-based FORTRAN 90 compiler).
- Should have some background or understanding of biochemical reaction kinetics. Note: Inappropriate kinetic expressions and/or kinetic constants may lead to unpredictable code behavior.
- Should be familiar with contaminant transport equations and coupled nonlinear differential equations.
References
- ^ Lu, G., Clement, T.P., Zheng, C., and Wiedemeier, T.H. (1999). Natural attenuation of BTEX compounds: Model development and field-scale application. Ground Water. 37(5):707–717.
- ^ Haggerty, R., and Gorelick, S.M. (1994). Design of Multiple Contaminant Remediation: Sensitivity to Rate-Limited Mass Transport. Water Resource Research, 30(2), 435–446.
- ^ See Clement, T.P., Sun., Y., Hooker, B.S., and Petersen, J.N. (Spring 1998). Modeling Multi-species Reactive Transport in Groundwater Aquifers, Groundwater Monitoring & Remediation Journal, 18(2), 79–92.
- ^ Baveye, P. and Valocchi, A.J. (1989). An Evaluation of Mathematical Models of the Transport of Biologically Reacting Solutes in Saturated Soils and Aquifers. Water Resources Research, 25(6): 1413–1421.
- ^ Taylor, S.W., and Jaffé, P.R. (1990). Substrate and Biomass Transport in a Porous Medium. Water Resources Research, 26(9): 2181–2194.
- ^ Hornberger, G.M., Mills, A.L., and Herman, J.S. (1992). Bacterial Transport in Porous Media: Evaluation of a Model Using Laboratory Observations. Water Resources Research, 28(3): 915-938.
- ^ Clement, T.P., Hooker, B.S., and Skeen, R.S. (1996). Macroscopic Models for Predicting Changes in Saturated Porous Media Properties Caused by Microbial Growth. Ground Water, 34(5): 934–942.
Related Topics
| [hide] GMS – Groundwater Modeling System | ||
|---|---|---|
| Modules: | 2D Grid • 2D Mesh • 2D Scatter Point • 3D Grid • 3D Mesh • 3D Scatter Point • Boreholes • GIS • Map • Solid • TINs • UGrids | |
| Models: | FEFLOW • FEMWATER • HydroGeoSphere • MODAEM • MODFLOW • MODPATH • mod-PATH3DU • MT3DMS • MT3D-USGS • PEST • PHT3D • RT3D • SEAM3D • SEAWAT • SEEP2D • T-PROGS • ZONEBUDGET | |
| Aquaveo | ||








![{\displaystyle r_{HC,O_{2}}=-k_{HC,O_{2}}[HC]{\frac {O_{2}}{K_{O_{2}}+[O_{2}]}}}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/07e297811cb2c0f9ef4214384afb27280b795ff3)
![{\displaystyle r_{HC,NO_{3}}=-k_{HC,NO_{3}}[HC]{\frac {NO_{3}}{K_{NO_{3}}+[NO_{3}]}}\bullet {\frac {K_{i,O_{2}}}{K_{i,O_{2}}+[O_{2}]}}}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/8c824050b9f3bb74514c556e4ba636d4ff4be533)
![{\displaystyle r_{HC,Fe^{3+}}=-k_{HC,Fe^{3+}}[HC]{\frac {Fe^{3+}}{K_{Fe^{3+}}+[Fe^{3+}]}}\bullet {\frac {K_{i,O_{2}}}{K_{i,O_{2}}+[O_{2}]}}\bullet {\frac {K_{i,NO_{3}}}{K_{i,NO_{3}}+[NO_{3}]}}}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/05bffb0755e3e5ec4efa6b60003b85dc9cebf01c)
![{\displaystyle r_{HC,SO_{4}}=-k_{HC,SO_{4}}[HC]{\frac {SO_{4}}{K_{SO_{4}}+[SO_{4}]}}\bullet {\frac {K_{i,O_{2}}}{K_{i,O_{2}}+[O_{2}]}}\bullet {\frac {K_{i,NO_{3}}}{K_{i,NO_{3}}+[NO_{3}]}}\bullet {\frac {K_{i,Fe^{3+}}}{K_{i,Fe^{3+}}+[Fe^{3+}]}}}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/ab50eefcff5226542b1ee3fe74f5e555dc085c2d)
![{\displaystyle r_{HC,CH_{4}}=-k_{HC,CH_{4}}[HC]{\frac {CO_{2}}{K_{CH_{4}}+[CO_{2}]}}\bullet {\frac {K_{i,O_{2}}}{K_{i,O_{2}}+[O_{2}]}}\bullet {\frac {K_{i,NO_{3}}}{K_{i,NO_{3}}+[NO_{3}]}}\bullet {\frac {K_{i,Fe^{3+}}}{K_{i,Fe^{3+}}+[Fe^{3+}]}}\bullet {\frac {K_{i,SO_{4}}}{K_{i,SO_{4}}+[SO_{4}]}}}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/fe7f233c8fdbfe7eb730f8307439be3b37c0ffbb)
![{\displaystyle [Fe^{3+}]=[Fe^{2+_{max}}]-[Fe^{2+}]}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/911a425ba74251e026c259a25871ee786bde0c50)
![{\displaystyle [MC]=[CO_{2}]=[CH_{4,max}]-[CH_{4}]}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/e4f36de8ab9eb7b4ee667d3d65d1ea7841d7b649)
![{\displaystyle {\frac {d[HC]}{dt}}=r_{HC,O_{2}}+r_{HC,NO_{3}}+r_{HC,Fe^{2+}}+r_{HC,SO_{4}}+r_{HC,CH_{4}}}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/3e6971366d6e23ab000cc719871eb235e26099cb)
![{\displaystyle {\frac {d[O_{2}]}{dt}}=Y_{O_{2}/HC}\;r_{HC,O_{2}}}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/1f978e7d5572eb3c1d9c873f656ae9a70d31c804)
![{\displaystyle {\frac {d[NO_{3}]}{dt}}=Y_{NO_{3}/HC}\;r_{HC,NO_{3}}}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/431b2bf13e7215aba242d44110e82ea07c413d3c)
![{\displaystyle {\frac {d[Fe^{2+}]}{dt}}=Y_{Fe^{2+}/HC}\;r_{HC,Fe^{2+}}}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/6e3d5a445db42211d602d668d0c7311208da7d4e)
![{\displaystyle {\frac {d[SO_{4}]}{dt}}=Y_{SO_{4}/HC}\;r_{HC,SO_{4}}}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/7314ea20e0a610b3dd6a982a78bea59e09fd1f44)
![{\displaystyle {\frac {d[CH_{4}]}{dt}}=Y_{CH_{4}/HC}\;r_{HC,CH_{4}}}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/d50ef4e4a911d551c724d72643ec41e778240f66)





![{\displaystyle R_{D}{\frac {\partial [D]}{\partial t}}={\frac {\partial }{\partial _{X_{i}}}}{\biggl (}D_{ij}{\frac {\partial [D]}{\partial _{X_{j}}}}{\biggr )}-{\frac {\partial }{\partial _{X_{i}}}}(v_{i}[D])+{\frac {q_{s}}{\Phi }}[D_{s}]-\mu _{m}{\biggl (}[X]+{\frac {\rho {\tilde {X}}}{\Phi }}{\biggr )}{\biggl (}{\frac {[D]}{K_{D}+[D]}}{\biggr )}{\biggl (}{\frac {[A]}{K_{A}+[A]}}{\biggr )}}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/160921af7fc9e8dbdaa5f44b04d3c23ffe2789d4)
![{\displaystyle R_{A}{\frac {\partial [A]}{\partial t}}={\frac {\partial }{\partial _{X_{i}}}}{\biggl (}D_{ij}{\frac {\partial [A]}{\partial _{X_{j}}}}{\biggr )}-{\frac {\partial }{\partial _{X_{i}}}}(v_{i}[A])+{\frac {q_{s}}{\Phi }}[A_{s}]-Y_{A/D}\mu _{m}{\biggl (}[X]+{\frac {\rho {\tilde {X}}}{\Phi }}{\biggr )}{\biggl (}{\frac {[D]}{K_{D}+[D]}}{\biggr )}{\biggl (}{\frac {[A]}{K_{A}+[A]}}{\biggr )}}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/83f24f1c5a27b91b8299f4be06b6682993baa123)
![{\displaystyle {\frac {\partial [X]}{\partial t}}={\frac {\partial }{\partial _{X_{i}}}}{\biggl (}D_{ij}{\frac {\partial [X]}{\partial t}}{\biggr )}-{\frac {\partial }{\partial _{X_{i}}}}(v_{i}[X])+{\frac {q_{s}}{\Phi }}[X_{s}]-K_{att}[K]+{\frac {K_{der}\rho {\tilde {X}}}{\Phi }}+Y_{X/D}\mu _{m}[X]{\biggl (}{\frac {[D]}{K_{D}+[D]}}{\biggr )}{\biggl (}{\frac {[A]}{K_{A}+[A]}}{\biggr )}+K_{e}[X]}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/8060bdbc9717e45d2aef901def26d1539b322cb8)
![{\displaystyle {\frac {d{\tilde {X}}}{dt}}={\frac {K_{att}\Phi [X]}{\rho }}-K_{det}{\tilde {X}}+Y_{X/D}\mu _{m}{\tilde {X}}{\biggl (}{\frac {[D]}{K_{D}+[D]}}{\biggr )}{\biggl (}{\frac {[A]}{K_{A}+[A]}}{\biggr )}-K_{e}{\tilde {X}}}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/186f1ecba538f04c664e5fb83dee17eb182f8026)
![{\displaystyle {\frac {d[D]}{dt}}=-{\frac {\mu _{m}}{R_{D}}}{\biggl (}[X]+{\frac {\rho {\tilde {X}}}{\Phi }}{\biggr )}{\biggl (}{\frac {[D]}{K_{D}+[D]}}{\biggr )}{\biggl (}{\frac {[A]}{K_{[A]}+[A]}}{\biggr )}}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/be44e09707c0c2da6cff683b85e784bb4d5b1b13)
![{\displaystyle {\frac {d[A]}{dt}}=-{\frac {Y_{A/D}\mu _{m}}{R_{A}}}{\biggl (}[X]+{\frac {\rho {\tilde {X}}}{\Phi }}{\biggr )}{\biggl (}{\frac {[D]}{K_{D}+[D]}}{\biggr )}{\biggl (}{\frac {[A]}{K_{A}+[A]}}{\biggr )}}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/daa37ffb02712756c15643ca4dd1a2ea59bd1f8e)
![{\displaystyle {\frac {d[X]}{dt}}=-Y_{X/D}\mu _{m}{\biggl (}[X]+{\frac {\rho {\tilde {X}}}{\Phi }}{\biggr )}{\biggl (}{\frac {[D]}{K_{D}+[D]}}{\biggr )}{\biggl (}{\frac {[A]}{K_{A}+[A]}}{\biggr )}+{\frac {K_{det}\rho {\tilde {X}}}{\Phi }}-K_{att}[X]-K_{e}[X]}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/b61948a69dfc82bd211a2d18d24ff35c720e8c08)

![{\displaystyle r_{PCE}=-k_{1}[PCE]}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/55455da900143c0cb0bd9e915e954a868c9fb842)
![{\displaystyle r_{TCE}=k_{1}Y_{TCE/PCE}[PCE]-k_{2}[TCE]}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/4c3a4e1d6b3dc6dc84ab0305a77c55236a3e1cbf)
![{\displaystyle r_{DCE}=k_{2}Y_{DCE/TCE}[TCE]-k_{3}[DCE]}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/fc24b923447e8e78784d071670233d449f75bd64)
![{\displaystyle r_{DCE}=k_{3}Y_{VC/DCE}[DCE]-k_{4}[VC]}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/85dfd8e184eaec992aa03e297eb0022894e80295)