WMS:Rational Method Equation
The rational method is used around the world for peak flow estimation of small rural drainage basins and is the most widely used method for urban drainage design. The rational method equation is given below:
- $ Q=kCiA_{}^{} $
- where:
- Q – Peak flow (cfs or m^3/s).
- k – Conversion factor equal to 1.008 (SI) or .00278 (metric).
- C – Dimensionless runoff coefficient.
- i – Rainfall intensity (in/hr, mm/hr).
- A – Catchment area (acres, ha).
The rational method is generally considered to be an approximate model for computing the flood peak resulting from a given rainfall, with the runoff coefficient accounting for all differences between the rainfall intensity and the flood peak. Such differences result from infiltration, temporary storage, and other losses. A table of C values recommended by the American Society of Civil Engineers and Water Pollution Control Federation is found in the article Runoff Coefficient Table.
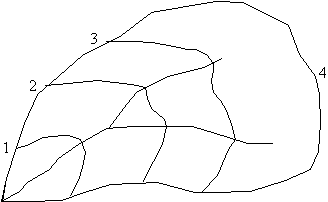
The rational equation was developed from a simplified analysis of runoff using isochrones, or lines of equal travel time with areas in acres between them as illustrated in the figure below. The method assumes no temporary storage in the basin, so the ratio between the peak runoff and the rainfall intensity is then the same as the ratio of the volumes of runoff and rainfall. If a constant rainfall intensity (in/hr) begins at time t=0 and has a duration of the time of concentration (tc) for the basin, the hydrograph will reach an instantaneous peak at Ci. The tc of the basin can be thought of as the time after rainfall excess begins to when all portions of the watershed are contributing to the peak flow at the outlet. If the duration is longer than tc, the hydrograph will remain constant after reaching a value of Ci for a time period equal to the difference of the rainfall duration and tc. In either case the time of rise and time of recession are equal to tc.
With such a derivation, the effects of rainfall and basin size are accounted for explicitly, while most other physical characteristics of the watershed are accounted for indirectly by the time of concentration and runoff coefficient. This simple equation illustrates the critical nature of tc. For durations less than tc, the entire area is not contributing. For durations larger than tc there is no increase in contributing area, and therefore no increase in peak flow.
Related Topics
- Important Limitations
- Runoff Coefficient Table
- Entering Rational Method Parameters
- Computing Hydrographs with Rational Method
| [hide] WMS – Watershed Modeling System | ||
|---|---|---|
| Modules: | Terrain Data • Drainage • Map • Hydrologic Modeling • River • GIS • 2D Grid • 2D Scatter |  |
| Models: | CE-QUAL-W2 • GSSHA • HEC-1 • HEC-HMS • HEC-RAS • HSPF • MODRAT • NSS • OC Hydrograph • OC Rational • Rational • River Tools • Storm Drain • SMPDBK • SWMM • TR-20 • TR-55 | |
| Toolbars: | Modules • Macros • Units • Digitize • Static Tools • Dynamic Tools • Drawing • Get Data Tools | |
| Aquaveo | ||